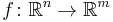Sard's theorem

Sard's theorem, also known as Sard's lemma or the Morse–Sard theorem, is a result in mathematical analysis which asserts that the image of the set of critical points of a smooth function f from one Euclidean space or manifold to another has Lebesgue measure 0 – they form a null set. This makes it "small" in the sense of a generic property.

Contents

Statement

More explicitly (Sternberg (1964, Theorem II.3.1); Sard (1942)), let

f\colon \mathbb{R}^n \rightarrow \mathbb{R}^m

be Ck, k times continuously differentiable, where k ≥ max{n−m+1, 1}. Let X be the critical set of f, the set of points x in Rn at which the Jacobian matrix of f has rank < m. Then f(X) has Lebesgue measure 0 in Rm.

Thus although X itself may be large, its image must be small: f may have many critical points (in the domain Rn), it has few critical values (in the target space Rm).

More generally, the result also holds for mappings between second countable differentiable manifolds M and N of dimensions m and n, respectively. The critical set X of a Ck function f : N → M consists of those points at which the differential df : TN → TM has rank less than m as a linear transformation. If k ≥ max{n−m+1, 1}, then Sard's theorem asserts that the image of X has measure zero as a subset of M. This formulation of the result follows from the version for Euclidean spaces by taking a countable set of coordinate patches. The conclusion of the theorem is a local statement, since a countable union of sets of measure zero is a set of measure zero, and the property of a subset of a coordinate patch having zero measure is invariant under diffeomorphism.

Variants

There are many variants of this lemma, which plays a basic role in singularity theory among other fields. The case m = 1 was proven by Anthony P. Morse in 1939 (Morse 1939), and the general case by Arthur Sard in 1942 (Sard 1942).

A version for infinite-dimensional Banach manifolds was proven by Stephen Smale (Smale 1965).

The statement is quite powerful, and the proof is involved analysis. In topology it is often quoted — as in the Brouwer fixed point theorem and some applications in Morse theory — in order to use the weaker corollary that “a non-constant smooth map has a regular value”, and sometimes “...hence also a regular point”.

In 1965 Sard further generalized his theorem to state that if f : M → N is Ck for k ≥ max{n−m+1, 1} and if Ar ⊆ M is the set of points x ∈ M such that dfx has rank less than or equal to r then f(Ar) has Hausdorff dimension at most r.

See also

References